在时间序列分析中，单位根检验是判断数据平稳性的核心步骤。EViews作为一款强大的计量经济学软件，为我们提供了多种单位根检验方法，如ADF检验、PP检验和KPSS检验，帮助分析时间序列数据的平稳性。本文将围绕EViews单位根检验如何操作EViews单位根检验模型选择与结果解读步骤进行详细讲解，并提供实用技巧和操作步骤。

　　一、EViews单位根检验如何操作

　　单位根检验是判断时间序列平稳性的重要步骤。如果时间序列存在单位根，意味着数据非平稳，直接建模可能导致虚假回归。

　　通过单位根检验，可以确定差分次数，使数据达到平稳性要求。

　　1.常见单位根检验方法

　　（1）ADF（Augmented Dickey-Fuller）检验

　　用途：检测时间序列中是否存在单位根。

　　特点：适用于存在自相关的时间序列。

　　优点：可处理高阶滞后项，减少自相关干扰。

　　（2）PP（Phillips-Perron）检验

　　用途：针对异方差性和自相关性的改进。

　　特点：不引入滞后项，直接校正序列的自相关和异方差。

　　优点：对长尾分布数据有较好效果。

　　（3）KPSS（Kwiatkowski-Phillips-Schmidt-Shin）检验

　　用途：检测序列的平稳性，假设序列平稳。

　　特点：适用于验证趋势平稳性，与ADF相反。

　　优点：可用于双重验证序列是否平稳。

　　2.单位根检验的准备工作

　　（1）数据准备

　　打开EViews，导入时间序列数据，如GDP增长率或股票价格。

　　确保数据格式为单变量时间序列，如季度数据或月度数据。

　　（2）数据平稳性检查

　　通过绘制时序图查看数据趋势和周期性。

　　使用自相关图（ACF）判断是否存在长期趋势。

　　3.EViews中进行ADF单位根检验

　　步骤一：选择检验变量

　　双击GDP增长率序列，打开数据窗口。

　　在窗口顶部选择View->Unit Root Test->Augmented Dickey-Fuller。

　　步骤二：设置检验参数

　　Test Type：选择ADF，表示进行扩展Dickey-Fuller检验。

　　Include in Test Equation：

　　None：不包含截距项，适用于完全平稳序列。

　　Intercept：包含常数项，适用于有截距无趋势序列。

　　Trend and Intercept：包含趋势和截距，适用于具有线性趋势序列。

　　Lag Length：选择自动滞后或手动设置滞后长度，一般根据AIC或BIC准则选择。

　　点击OK，EViews自动输出检验结果。

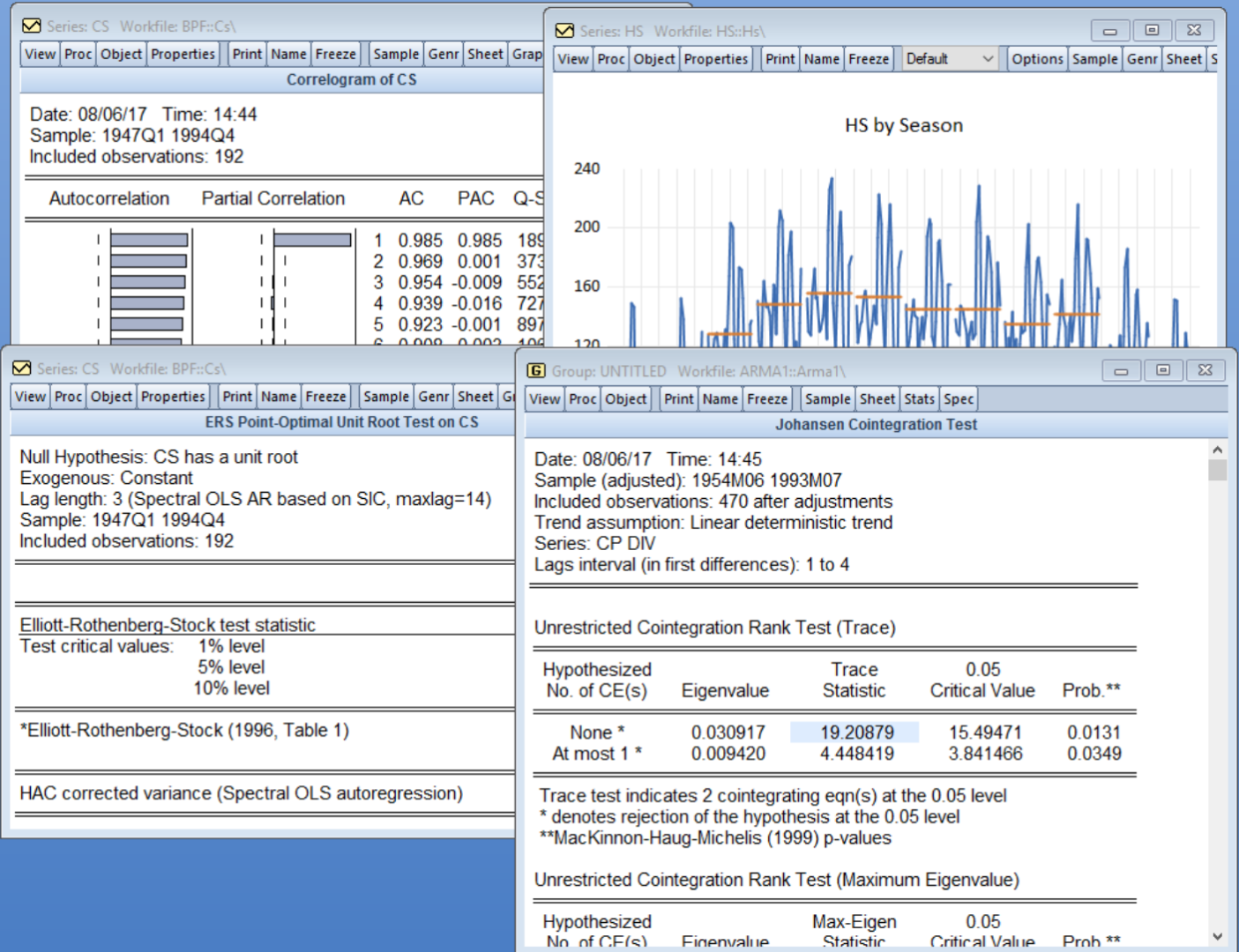
　　二、EViews单位根检验模型选择与结果解读步骤

　　1.如何选择合适的单位根检验模型

　　（1）根据数据特征选择模型

　　趋势存在：如果数据呈现线性趋势，选择Trend and Intercept。

　　水平漂移：如果数据围绕固定均值波动，选择Intercept。

　　完全平稳：数据无明显趋势，选择None。

　　（2）根据信息准则调整滞后阶数

　　AIC（Akaike Information Criterion）：越小越好，适合中小样本。

　　BIC（Bayesian Information Criterion）：越小越好，适合大样本。

　　HQ（Hannan-Quinn Criterion）：平衡精度和简洁性。

　　滞后阶数选择不当，可能导致假阳性或假阴性结果。

　　2.EViews单位根检验结果解读

　　（1）关键检验指标解读

　　ADF Test Statistic：检验值与临界值对比，判断是否拒绝原假设。

　　Test Critical Values：

　　1%：严格拒绝标准

　　5%：中等拒绝标准

　　10%：宽松拒绝标准

　　P-value：

　　P<0.05：拒绝原假设，序列平稳

　　P≥0.05：不拒绝原假设，序列非平稳

　　（2）结果解读示例

　　解读：

　　ADF统计量（-3.12）小于5%临界值（-2.89），拒绝原假设，序列平稳。

　　如果P值<0.05，也支持平稳性假设。

　　3.双重验证平稳性的策略

　　（1）使用PP检验进行验证

　　通过Phillips-Perron检验，再次验证序列平稳性。

　　如果ADF和PP结果一致，说明序列平稳性可靠。

　　（2）使用KPSS检验对照

　　KPSS假设序列平稳，与ADF相反。

　　如果KPSS拒绝原假设，而ADF不拒绝，说明序列非平稳。

　　当KPSS和ADF结果相反时，优先使用KPSS结果。

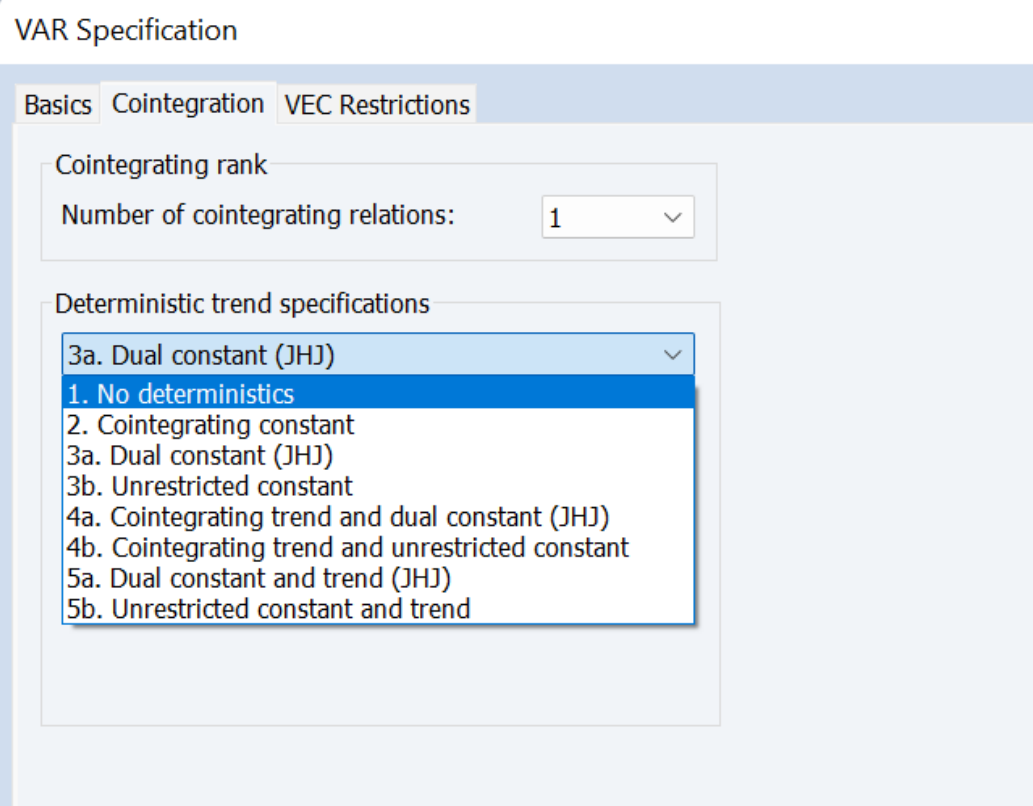
　　三、单位根检验在时间序列分析中的重要性

　　在时间序列建模中，单位根检验是判断序列平稳性的基础环节。

　　如果不进行单位根检验，直接建模可能导致模型误判和虚假回归，尤其在经济指标预测和金融数据分析中，平稳性检验至关重要。

　　1.单位根检验的重要性

　　模型准确性：确保模型参数估计准确，避免序列异方差。

　　预测可靠性：平稳序列预测效果更稳定，误差更小。

　　统计推断有效性：非平稳序列会导致回归系数不显著或系数估计偏误。

　　2.结合平稳性调整策略

　　差分法：对非平稳序列进行一阶或二阶差分，提升平稳性。

　　对数转换：针对指数增长或波动率，进行对数变换。

　　季节调整：对具有周期性特征的数据，进行季节性差分。

　　四、总结

　　在时间序列分析中，EViews单位根检验如何操作EViews单位根检验模型选择与结果解读步骤是模型构建和预测分析的关键步骤。通过合理选择单位根检验模型，结合ADF、PP和KPSS检验，可以准确判断序列的平稳性。实际操作中，根据检验结果调整模型结构，能够有效避免虚假回归，提升预测效果的科学性和可靠性。